පලවෙනි තෑගි ප්‍රශ්නෙට පිලිතුර මෙන්න! |

මීට දවස් කීපෙක කලින් පොඩි ප්‍රශ්නයක් ඇහුවනේ මං..  උත්තර දුන්න අය හරි උත්තරේ මොකක්ද කියලා දැනගන්න බලං ඉන්නවා කියලා දැනුනු නිසා තෑගි ප්‍රශ්නෙට පස්සෙ දාන්න හිතාගෙන හිටපු පෝස්ට් එක පැත්තකට දාල හරි උත්තරේ කියල හිටින්න හිතුනා,..

ප්‍රශ්නෙ මොකක්ද කියල මෙන්න මෙතැන ඔබල බලලම එන්නකෝ... ඒ පෝස්ට් එක දැක්කෙ නැති කවුරු හරි ඉන්නවනම් ඒ ලින්ක් එක හරහා ඒ පෝස්ට් එකට ගිහින් ප්‍රශ්නෙ කියවලා හරි උත්තරේ හොයාගෙන ආයෙ මේ පැත්තට එන්නකෝ තමන් හරි උත්තරේ හොයාගත්තද කියලා බලන්නත් එක්ක..
.
.
.

රයිටෝ,, ඔන්න එහෙනම් පලවෙනි ප්‍රශ්නෙට උත්තරේ හොයන විදිය තමයි මේ කියල දෙන්න යන්නෙ..

මේ ප්‍රශ්නෙදි සමචතුරස්‍ර කීයක් තියනවද කියල ගොඩාක් අය හොයාගෙන තිබුනා.. නමුත් කීප දෙනෙක්ට සමචතුරස්‍ර ගණන නිවැරදිවම කියන්න බැරිවෙලා තියනවා.. අර සමචතුරස්‍ර ගණන නිවැරදිව හොයාගත්ත අයගෙනුත් බහුතරේකට සෘජුකෝණාස්‍ර ගනන නිවැරදිව කියන්න බැරි වෙලා.. දැං අපි මේ ගැටලුව හිමීට ලිහමු..

සමචතුරස්‍ර ගණන සොයන ආකාරය..



පිලිවලක් තියාගෙන හෙව්වනම් බොහොම පහසුවෙන් හරි උත්තරේ ලැබෙනවා..

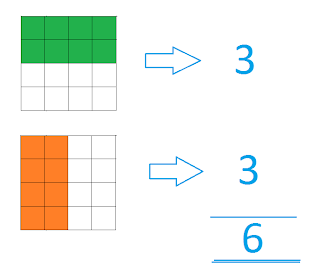
*කුඩා සමචතුරස්‍ර එක බැගින් කීයක් තියනවද??
*කුඩා සමචතුරස්‍ර 4ක් එකතු වෙලා හැදුනු සමචතුරස්‍ර කීයක් තියනවද?
*කුඩා සමචතුරස්‍ර 9 බැගින් එකතුවෙලා හැදුනු සමචතුරස්‍ර කීයක් තියනවද?
*කුඩා සමචතුරස්‍ර 16 බැගින් එකතු වෙලා හැදුනු සමචතුරස්‍ර කීයක් තියනවද? කියල හොයාගෙන ඒ ටික එකතු                   කලා නම් වැඩේ ගොඩ :)

සමචතුරස්‍ර 1 බැගින් 16ක් තියනවා කියලා බැලු බැල්මටම පේනවා.. උත්තරේ හොයන්න උත්සහ කරපු අය ඒ 16 අනිවාර්යෙන් දැක්කා.. ඒකෙ සැකයක් නෑ

ඊලඟට අපි බලමු සමචතුරස්‍ර 4 බැගින් එකතුවෙලා හැදුනු සමචතුරස්‍ර කීයක් තියනවද කියලා

සමචතුරස්‍ර 9ක් තියනවා.. මෙතනදි තමයි කට්ටියකට කීපයක් මග ඇරෙන්නෙ.. දුඹුරු පාටින් දක්වල තියන සමචතුරස්‍ර ගානත් හැමොම තමංගෙ ගණනය කිරීමට යොදාගන්නවා.. නමුත් කීප දෙනෙක්ට කොලපාටින් දක්වල තියන සමචතුරස්‍ර ගණන මග ඇරෙනවා.. ඒ අයගෙන් කීප දෙනෙක් තමයි 26යි කියලා උත්තරේ දීල තිබුනෙ..

ඒක ගනං කරගත්තු  අයගෙනුත් අන්තිමට ඔය නිල් පාටින් දක්වල තියන සමචතුරස්‍රය මග ඇරීමෙ සම්භාවිතාව ටිකක් වැඩියි.. මං හිතන්නෙ ඩූඩ් අයියට මග ඇරුන සමචතුරස්‍රය ඒක :) ඒකයි එයා 29යි කියල කිව්වෙ.

දැං ඊලඟට කුඩා සමචතුරස්‍ර 9 බැගින් එකතුවෙලා සෑදෙන සමචතුරස්‍ර  ගණන බලමු.

සමචතුරස්‍ර 4යි .. ඉහත අවස්තාවෙ සමචතුරස්‍ර 9යි කියපු අයට මේක මග ඇරුනෙ නෑ.. හැමෝම ඒක තමංගෙ ගණනනයට එකතු කරගත්තා..

ඊලඟට තව සමචතුරස්‍රයක් ඉතිරියි..



ඒ තමයි මේක :) ඒකත් හැමෝම දකිනවා. කිසිම විදියකින් මග ඇරෙන්නෙ නෑ..

මේ අනුව මුලු සමචතුරස්‍ර ගණන =  1 + 4 + 9 + 16
                               = 30 


කෙටි ක්‍රමය....

ඔන්න දැං හැමෝටම කෙටි ක්‍රමයක් පේන්න පටං අරං ඇති :).. මං ඉහත මුලු සමචතුරස්‍ර ගණන එකතුවක් විදියට පෙන්නුවෙත් ඒක පෙන්නන්න. ඇත්තම කිව්වොත් මේ ගැටලුව නිර්මාණය කරනකොට මං මේ කෙටි ක්‍රමය හොයාගෙන දැක්කෙ නෑ.. ඒත් තනියම  සමචතුරස්‍ර 25 බැගින් තියන එකකත් හෙව්වාම තමයි මං මේ කෙටි ක්‍රමය දැක්කෙ..

බලන්න ඉහත ගැටලුවෙ එක් තීරුවකට හෝ පේලියකට  සමචතුරස්‍ර 4 බැගින් තියනවා. එහෙනම් මුලු සමචතුරස්‍ර ගණන හොයන්න මුල් "වර්ග සංඛ්‍යා" (සමචතුරස්‍ර සංඛ්‍යා)  හතරේ එකතුව ගන්න විතරයි තියෙන්නෙ..

කෙටි ක්‍රමය පැහැදිලි කරගන්න තව චූටි උදාහරණයක් ගනිමු..

මෙතන සමචතුරස්‍ර කීයක් තියනවද??

හෝව්!! හෝව්! දැං ඉතින් පස්ස උඩ දාගෙන ගණං කරන්න දෙයක් නෑ.. අපිට තියනවා කෙටි ක්‍රමයක් :)

මෙතන තියෙන්නෙ එක පේලියකට සමචතුරස්‍ර 6 බැගින් තියන සමචතුරස්‍ර 36ක්.. එක පේලියකට 6 බැගින් තියන හින්දා අපිට කරන්න තියෙන්නෙ මුල් වර්ග සංඛ්‍යා 6යේ එකතුව හොයාගන්න එක විතරයි.. ගනං කිරීමක් කිසිසේත් අවශ්‍ය වන්නේ නෑ..

ඒ අනුව මුලු සමචතුරස්‍ර ගණන = 1 + 4 + 9 + 16 + 25 + 36
             =  91

හරි කෝම හරි කමක් නෑ මං අහපු ප්‍රශ්න දෙකෙන් පලවෙනි ප්‍රශ්නෙට උත්තරේ වන සමචතුරස්‍ර ගණන 30යි  කියලා නිවැරදි පිලිතුර දීල තියෙන්නෙ මෙන්න මේ අය .. හුරේ....... :D

1. Chandana 

2. සසිදු 

3. ඉවාන් පව්ලූශා ( Prageeth Anuradha )

4. SaKu PaTHi

5. Damith Gunawardane

6. සිහින සටහනේ ඉමල්ක

7. සු දී ක

8. Chams

9.  Hasini Weerakkody

10. ruwini wijesinghe

11. Chathura Panditha

12. DDT

13. rentere rewert

14. සයුරි

ඒ හැමෝටම ඔන්න මං ගානෙ points 2ක ගානෙ හම්බෙනවා.. ආ මෙන්න ගන්නෝ :D සුභ පැතුම් හැමෝටම!!!

--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

රායිට්.. දැං තමයි අමාරුම වැඩේ,, සෘජුකෝණාස්‍ර ගණන කීයද කියල හොයාගන්නයි ඕනෙ..
මේකට නං මට කෙටි ක්‍රමයක් පෙනුනෙ නෑ. කාලඟ හරි ඒම කෙටි ක්‍රමයක් තියෙනවනං කියන්න..

ඒත් නිවැරදි ක්‍රමයකට පිලිවලට සංයමයෙන් යුතුව ගනං කලොත් හරියටම කියන්න පුලුවන් සෘජුකෝනාස්‍ර කීයක් තියනවද කියලා
මේක ගොඩක් අයට වැරදෙන්න හේතුව තමයි ගණං කරන්න කිසි පිලිවලක් හදාගෙන නොතිබුනු එක. ඔහෙ තමන්ට පේන පේන එක එකයි දෙකයි තුනයි කියලා ගණං කරල නම් කවදාවත් කීයක් තියනවද කියලා හරියටම හොයන්න බෑ.. හොයාගත්ත අය ඒක හෙව්වෙ නියම පිලිවලට.. එතකොට අවුල් වෙන්නෙ නෑ ..

සෘජුකෝනාස්‍ර ගනං කරන එකත් අර සමචතුරස්‍ර මුලු ගණන හෙව්ව වගේම තමයි. ඉස්සෙල්ලම කරන්න ඕනි  සෘජුකෝනාස්‍ර  වර්ග කීයක් තියනවද කියලා හොයාගන්න එක.. ඊලඟට පුලුවන් ඒ වර්ගයකට සෘජුකෝණාස්‍ර කීය බැගින් තියනවද කියල හොයාගෙන එකතු කරන්න..

ඒ වගේම මෙතනදි එකින් එක ගණං කිරීම කිසිසේත් අවශ්ය වන්නේ නෑ.. රූප සටහන් ආස්‍රයෙන් පැහැදිලි කරනකොට තේරෙයි ඒකට හේතුව :)

ඒ අනුව රූපය දිහා බලපුවහම

*කුඩා සමචතුරස්‍ර 2ක බැගින් සෑදුනු සෘජුකෝනාස්‍ර 
*කුඩා සමචතුරස්‍ර 3 බැගින් සෑදුනු සෘජුකෝනාස්‍ර
*කුඩා සමචතුරස්‍ර 4 බැගින් සෑදුනු සෘජුකෝනාස්‍ර
*කුඩා සමචතුරස්‍ර 6 බැගින් සෑදුනු සෘජුකෝනාස්‍ර
*කුඩා සමචතුරස්‍ර 8 බැගින් සෑදුනු සෘජුකෝනාස්‍ර
*කුඩා සමචතුරස්‍ර 12 බැගින් සෑදුනු සෘජුකෝනාස්‍ර විදියට වර්ග 6ක් පෙනෙයි

දැං අපි මේ එක් එක් වර්ගයකට සෘජුකෝණාස්‍ර කීය ගානෙ තියනවද කියලා බලමු..

මුලින්ම කුඩා සමචතුරස්‍ර 2ක බැගින් සෑදුනු සෘජුකෝනාස්‍ර  කීයක් තියනවද බලමු..

මෙතනදි අපි ඉස්සෙල්ලම කරන්නෙ තීරුවකට කුඩා සමචතුරස්‍ර 2ක බැගින් සෑදුනු සෘජුකෝනාස්‍ර කීයක් ගානෙ තියනවද කියලා බලන එක

    
එක් තීරුවක සෘජුකෝනාස්‍ර 3ක් තියන බව ඔයාලට පේනවා. එලෙස 3 බැගින් තීරු 4ක් තියනවා.. එතකොට ඔක්කොම 12ක් තියනවා (3*4)

ඒ වගේම පේලියකට 3 බැගින් පේලි 4ටත් 12ක් තියන බව ඔයාලට පෙනේවි

 

ඒ අනුව කුඩා සමචතුරස්‍ර 2ක බැගින් සෑදුනු සෘජුකෝනාස්‍ර 24ක් තියනවා කියල දැකගන්න පුලුවන්

මේ විදියට තමයි අනිත් සෘජුකෝනාස්‍ර ගනන හොයාගන්නෙත්.. එකින් එක ගනං කිරීමක් කිසිසේත් කලයුතු නෑ..

දැං ඉතින් ඔයාලට කීයක් තියනවද කියල හොයාගන්න පුලුවන් උනත් මං හැමොටම පැහැදිලි වෙන්න රූප සටහන් ඇසුරෙන් ගනනය කරන හැටි පෙන්නන්නම්..

මේ විදියටම කුඩා සමචතුරස්‍ර 3 බැගින් සෑදුනු සෘජුකෝනාස්‍ර කීයක් තියනවද??

තීරුවකට 2යි. තීරු 4යි . තීරුවල 8යි. ඒනම් පේලිවලත් 8යි. ඔක්කොම 16ක් තියනවා කියලා පැහැදිලියි..ආයෙ අමුතුවෙන් පැහැදිලි කිරිමක් අවශ්‍ය වෙන්නෙ නෑ කියල හිතනවා ඉහත 'කුඩා සමචතුරස්‍ර 2ක බැගින් සෑදුනු සෘජුකෝනාස්‍ර ' කි‍යක් තියනවද කියල පැහැදිලි කරපු විදියටම තමයි මෙතනත් ගනනය සිදුකලයුතු වන්නේ..

ඊලගට කුඩා සමචතුරස්‍ර 4 බැගින් සෑදුනු සෘජුකෝනාස්‍ර ගනනත් මේ විදියටමයි..

තීරුවකට එකයි තීරු හතරටම 4යි. ඒනම් පේලි වලත් 4යි. ඔක්කොම 16යි

ඊලගට කුඩා සමචතුරස්‍ර 6 බැගින් සෑදුනු සෘජුකෝනාස්‍ර ගනන සොයමු

තිරස් අතට 6යි. ඒවගේම සිරස් අතටත් 6යි. ඔක්කොම 12යි.. ඉහත පෙන්නල තියෙන්නෙ තිරස් අතට තියන ගණන විතරයි. සිරස් අතටත් එලෙසම සෙවිය යුතු  බව දක්වා තිබෙනවා රෝස පාට රූපෙන්..

කුඩා සමචතුරස්‍ර 8 බැගින් සෑදුනු සෘජුකෝනාස්‍ර ගණන ...

තිරස් අතට 3යි.. සිරස් අතට 3යි ඔක්කොම 6යි.
පැහැදිලි නැත්නම් මීට පෙර රූප සටහනේ තිරස් අතට හෙව්ව හැටි දක්වා තිබෙනවා .. බලන්න

අන්තිමට කුඩා සමචතුරස්‍ර 12 බැගින් සෑදුනු සෘජුකෝනාස්‍ර 

4ක් තියනවා කියලත් පේනවා..

දැං ඉතින් ඔක්කොම හොයලා ඉවරයි .. එකතු කරන්න විතරයි තියෙන්නෙ..

කුඩා සමචතුරස්‍ර 2ක බැගින් සෑදුනු සෘජුකෝනාස්‍ර  = 24
කුඩා සමචතුරස්‍ර 3 බැගින් සෑදුනු සෘජුකෝනාස්‍ර      = 16
කුඩා සමචතුරස්‍ර 4 බැගින් සෑදුනු සෘජුකෝනාස්‍ර       = 8
කුඩා සමචතුරස්‍ර 6 බැගින් සෑදුනු සෘජුකෝනාස්‍ර       = 12
කුඩා සමචතුරස්‍ර 8 බැගින් සෑදුනු සෘජුකෝනාස්‍ර       = 6
කුඩා සමචතුරස්‍ර 12 බැගින් සෑදුනු සෘජුකෝනාස්‍ර     = 4

                 ඔක්කොම = 70යි                            

සමහර විට පැහැදිලි කිරීම දිහා බලං ඉදලා මේ මොන විකාරයක්ද කියලා හිතෙයි. නමුත් හොදින් කියෙව්වොත් එකින් එක එකයි දෙකයි තුනයි කියලා ගණනය නොකර මුලු සෘජුකෝනාස්‍ර ගනන 70යි කියන උත්තරේ ලබා ගන්න පුලුවන් හරිම ලේසියෙන්. :)

සෘජුකෝණාස්‍ර ගණන හරියටම කියල තිබුනෙත් ඒ අනුව ප්‍රශ්න දෙකටම නිවැරදිව පිලිතුරු දීල තිබුනෙත්  මෙන්න මේ දෙන්නා විතරයි .. හුරේ!!!!

සු දී ක

ruwini wijesinghe

ඒ දෙන්නට points 5ක් ඔන්න ලැබෙනවා මේ තෑගි ප්‍රශ්නෙදි.. සුභ පැතුම් දෙන්නටම !! අනිත් අය දුක් වෙන්න ඕනි නෑ.. ඉස්සරහට අහන ඒවට උත්තර දීලා points එකතු කරගන්න පුලුවන්..

හරි ගියත් වැරදුනත් උත්තර දුන්නු හැමදෙනාටමත්, උත්සහ කල හැමදෙනාටමත් කම්න්ට්ස් කරපු හැම දෙනාටමත් බෙහෙවින්ම ස්තූතියි!!!!
නැවත තෑගි ප්‍රශ්නෙකින් හමුවෙමු...
(ඊලග පෝස්ට් එක තෑගි ප්‍රශ්නයක් නං නෙමෙයි ඕං)